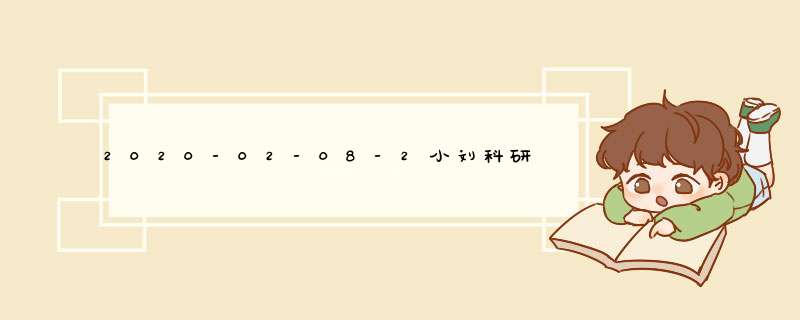
以目前实验室配有的FIB-SEM的型号是蔡司的Crossbeam 540为例进行如下分析,离子束最高成像分辨率为3nm,电子束最高分辨率为0.9nm。该系统的主要部件及功能如下:
1.离子束: 溅射(切割、抛光、刻蚀);刻蚀最小线宽10nm,切片最薄3nm。
2.电子束 : 成像和实时观察
3.GIS(气体注入系统): 沉积和辅助刻蚀;五种气体:Pt、W、SiO2、Au、XeF2(增强刻蚀SiO2)
4.纳米机械手: 转移样品
5.EDS: 成分定量和分布
6.EBSD : 微区晶向及晶粒分布
7.Loadlock(样品预抽室): 快速进样,进样时间只需~1min
由上述FIB-SEM的一个部件或多个部件联合使用,可以实现在材料研究中的多种应用,具体应用实例如下:
图2a和b分别是梳子形状的CdS微米线的光学显微镜和扫描电镜照片,从光学显微镜照片可以看出在CdS微米线节点处内部含有其他物质,但无法确定是什么材料和内部形貌。利用FIB-SEM在节点处定点切割截面,然后对截面成像和做EDS mapping,如图2c、d、e和f所示,可以很直观的得到在CdS微米线的节点处内部含有Sn球。
FIB-SEM制备TEM样品的常规步骤如图3所示,主要有以下几步:
1)在样品感兴趣位置沉积pt保护层
2)在感兴趣区域的两侧挖大坑,得到只有约1微米厚的薄片
3)对薄片进行U-cut,将薄片底部和一侧完全切断
4)缓慢移下纳米机械手,轻轻接触薄片悬空的一端后,沉积pt将薄片和纳米机械手焊接牢固,然后切断薄片另一侧,缓慢升起纳米机械手即可提出薄片
5)移动样品台和纳米机械手,使薄片与铜网(放置TEM样品用)轻轻接触,然后沉积pt将薄片和铜网焊接牢固,将薄片和纳米机械手连接的一端切断,移开纳米机械手,转移完成
6)最后一步为减薄和清洗,先用大加速电压离子束将薄片减薄至150nm左右,再利用低电压离子束将其减薄至最终厚度(普通TEM样品<100nm,高分辨TEM样品50nm左右,球差TEM样品<50nm)
一种如图4a所示的MoS2场效应管,需要确定实际器件中MoS2的层数及栅极(Ag纳米线)和MoS2之间的距离。利用FIB-SEM可以准确的在MoS2场效应管的沟道位置,垂直于Ag纳米线方向,提出一个薄片,并对其进行减薄,制备成截面透射样。在TEM下即可得到MoS2的层数为14层(图4c), Ag纳米线和MoS2之间的距离为30nm(图4b)。
图5是一种锰酸锂材料的STEM像,该样品是由FIB-SEM制备,图中可以看到清晰的原子像。这表明FIB-SEM制备的该球差透射样非常薄并且有很少的损伤层。
FIB-SEM还可以进行微纳图形的加工。
图6a 是FIB-SEM在Au/SiO2上制备的光栅,光栅周期为150nm,光栅开口为75nm。
图6b 是利用FIB-SEM在Mo/石英上做的切仑科夫辐射源针尖,针尖曲率半径为17nm。
图6c 是在Au膜上加工的三维对称结构蜘蛛网。
图6d 是FIB-SEM在硅上刻蚀的贺新年图案,图中最小细节尺寸仅有25nm。
FIB-SEM可以对材料进行切片式的形貌和成分三维重构,揭示材料的内部三维结构。大概过程如图7a所示, FIB切掉一定厚度的样品,SEM拍一张照片,重复此过程,连续拍上百张照片,然后将上百张切片照片重构出三维形貌。图7b是一种多孔材料内部3×5×2um范围的三维重构结果,其实验数据是利用FIB-SEM采集,三维重构是利用Avizo软件得到,其分辩率可达纳米级,展示了内部孔隙的三维空间分布,并可以计算出孔隙的半径大小、体积及曲率等参数。
利用FIB-SEM配有的纳米机械手及配合使用离子束沉积Pt,可以实现微米材料的转移,即把某种材料从一个位置(衬底)转移到特定位置(衬底),并固定牢固。图8是把四针氧化锌微米线从硅片转移到两电极的沟道之间,从而制备成两个微米线间距只有1um的特殊器件。
最后,FIB-SEM还有很多其他的应用,例如三维原子探针样品制备,芯片线路修改等。总之FIB-SEM是材料研究中一个非常重要的手段。
不积珪步,无以至千里;不积细流,无以成江海。做好每一份工作,都需要坚持不懈的学习。
SEM简单介绍,以下资料来源
因果关系:SEM一般用于建立因果关系模型,但是本身却并不能阐明模型的因果关系。
一般应用于:测量错误、错漏的数据、中介模型(mediation model)、差异分析。
历史:SEM 包括了 回归分析,路径分析(wright, 1921),验证性因子分析(confirmatory factor analysis)(Joreskog, 1969).
SEM也被称为 协方差结构模型(covariance structure modelling),协方差结构分析和因果模型。
因果关系:
究竟哪一个是“真的”? 在被假设的因果变量中其实有一个完整的因果链。
举一个简单的例子: 吃糖果导致蛀牙。这里涉及2个变量,“吃糖果”和“蛀牙”,前者是因,后者是果。 如果上一个因果关系成立,那将会形成一个因果机制,也许会出现这样的结构:
3. 这时还有可能出现更多的潜在变量:
这里我又举另外一个例子,回归模型
在这里,回归模型并不能很好的描述出因果次序,而且也不能轻易的识别因果次序或者未测量的因子。这也是为什么在国外学术界SEM如此流行的原因。
我们在举另外一个例子“路径分析”
路径分析能让我们用于条件模型(conditional relationships),上图中的模型是一种调解型模型或者中介模型,在这里Z 是作为一个中介调节者同时调节X和Y这两个变量的关系。
在这里我们总结一下:
回归分析简单的说就是:X真的影响Y 吗?
路径分析:为什么/如何 X 会影响Y? 是通过其他潜在变量Z 来达到的吗?例子:刷牙(X)减少蛀牙(Y)通过减少细菌的方法(Z)。------测量和测试中介变量(例如上图中的Z变量)可以帮助评估因果假设。
在这里要提一下因素模型(factor model)
在这个模型当中,各个变量有可能由于受到未被观察到的变量所影响,变得相互有内在的联系,一般来说那些变量都很复杂、混乱,而且很多变量是不能直接被观察到的。
举个例子:“保龄球俱乐部的会员卡”和“本地报纸阅读”,是被观察到的变量,而“社会资产”则是未被观察到的变量。另一个例子:“房屋立法”和“异族通婚”是被观察到的变量,而“种族偏见”是未被观察到的变量。
相互关系并不完全由被观察到的变量的因果关系所导致,而是由于那些潜在的变量而导致。
这些被观察到变量(y1--y4)也有可能由一个潜在的变量(F)所影响。
欢迎分享,转载请注明来源:夏雨云

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)